7.4 Transformações
Nesta seção definiremos as matrizes de transformação em coordenadas homogêneas que correspondem às principais transformações afins utilizadas no pipeline de renderização.
Identidade
A transformação de identidade é a transformação que mapeia um ponto a ele mesmo:
\[ \mathbf{p}'=\mathbf{p}. \]
É representada por uma matriz identidade:
\[ \mathbf{I}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}. \] Assim,
\[ \mathbf{p}'=\mathbf{I}\mathbf{p}=\mathbf{p}. \]
Translação
Translação é a transformação afim de deslocamento de um ponto \(\mathbf{p}\) por um vetor \(\mathbf{t}\):
\[ \mathbf{p}'=\mathbf{p}+\mathbf{t} \]
\[ \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix}= \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}+ \begin{bmatrix} t_x \\ t_y \\ t_z \\ 0 \end{bmatrix}. \]
A figura 7.2 ilustra o resultado da translação de todos os pontos de um cubo centralizado na origem.
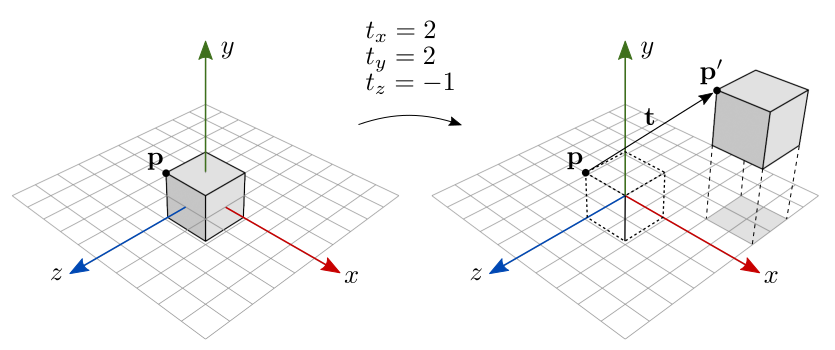
Figura 7.2: Translação.
A matriz de translação é definida como
\[ \mathbf{T}=\mathbf{T}(\mathbf{t})= \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}. \]
Assim,
\[ \mathbf{p}'=\mathbf{T}\mathbf{p} \]
\[ \begin{bmatrix} x+t_x\\ y+t_y\\ z+t_z\\ 1\end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1\end{bmatrix}. \]
A inversa da translação é o deslocamento de \(\mathbf{p}\) no sentido inverso do vetor de deslocamento:
\[ \mathbf{T}^{-1}(\mathbf{t})=\mathbf{T}(-\mathbf{t}). \]
Note que a transformação de translação não altera o formato do objeto. O objeto deslocado continua com as mesmas proporções. Uma transformação que, como a translação, preserva a distância entre todos os pontos do objeto transformado, é chamada de transformação de corpo rígido.
Escala
A escala é um tipo de transformação linear que faz com que um objeto aumente ou diminua de tamanho de acordo com fatores de escala em \(x\), \(y\) e \(z\). Desse modo, a escala não é uma transformação de corpo rígido.
A transformação de escala é obtida multiplicando cada coordenada \((x,y,z)\) de um ponto \(\mathbf{p}\) pelos escalares \((s_x, s_y, s_z)\):
\[ \begin{align} x' &= s_x x\\ y' &= s_y y\\ z' &= s_z z. \end{align} \]
Se os fatores de escala forem todos iguais (\(s_x=s_y=s_z\)), temos uma escala uniforme pois o objeto é redimensionado por igual em todas direções. A figura 7.3 ilustra o resultado da escala uniforme de cada ponto de um cubo centralizado na origem. Como \(s_x=s_y=s_z=2\), o objeto dobra de tamanho em cada dimensão.
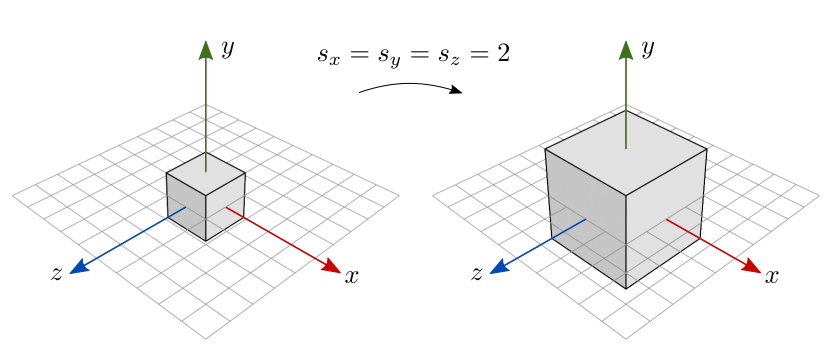
Figura 7.3: Escala uniforme sobre um objeto centralizado na origem.
A origem do frame é o ponto fixo da transformação, isto é, é o ponto que não é afetado pela escala. Observe, na figura 7.4, a escala uniforme de um cubo que não está centralizado na origem. O vértice que coincide com a origem é o único ponto que permanece inalterado. Pontos na origem continuam na origem após a escala.
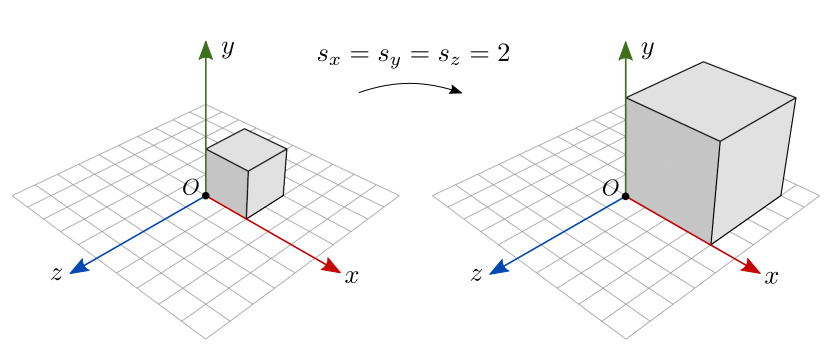
Figura 7.4: Escala uniforme sobre um objeto não centralizado na origem.
Antes da aplicação da transformação de escala, é frequentemente desejável centralizar o objeto na origem ou fazer com que pelo menos a base do objeto fique centralizada na origem, como no modelo mostrado na figura 7.5.
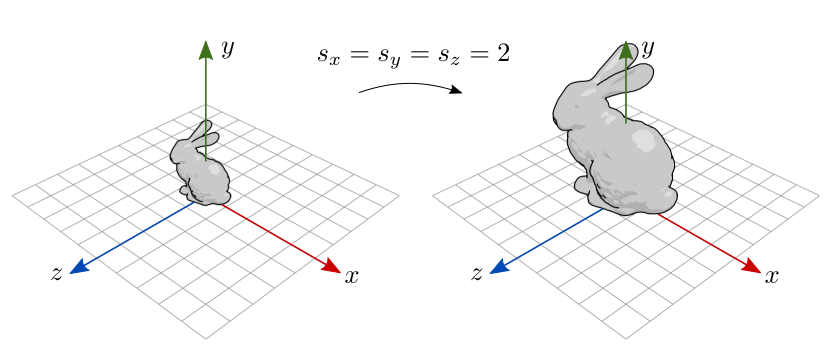
Figura 7.5: Escala em objeto com base centralizada na origem.
Se o objeto não estiver centralizado na origem, a escala poderá deslocar o objeto de forma indireta. Por exemplo, se um cubo unitário estiver centralizado no ponto \((10,10,10)\), a escala com \(s_x=s_y=s_z=2\) dobrará o tamanho do cubo em cada dimensão, como esperado. Porém, o cubo agora estará centralizado no ponto \((20,20,20)\), o que provavelmente não é o que se quer.
Se os fatores de escala estão no intervalo \([0, 1)\), o objeto diminui de tamanho. A figura 7.6 mostra o resultado de uma escala uniforme que diminui o tamanho do objeto. Como \(s_x=s_y=s_z=0.5\), o objeto resultante tem \(50\%\) do tamanho original em cada dimensão.
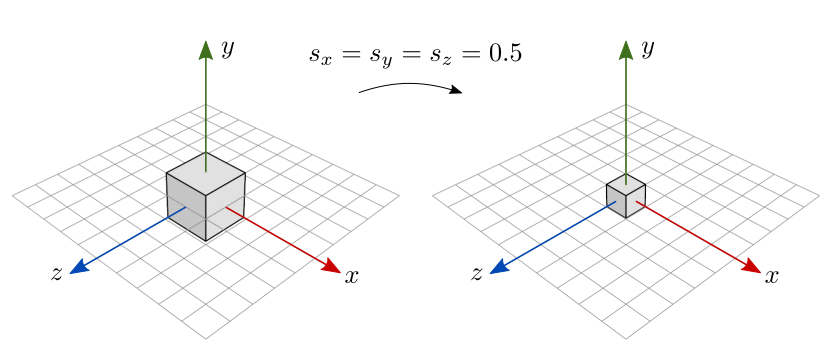
Figura 7.6: Escala uniforme com fatores de escala menores que 1.
Se os fatores de escala não são iguais, o resultado é uma escala não uniforme. Na figura 7.7, o cubo triplica de tamanho na direção \(x\) (\(s_x=3\)), mantém o tamanho na direção \(y\) (\(s_y=1\)), e diminui o tamanho pela metade em \(z\) (\(s_z=0.5\)).
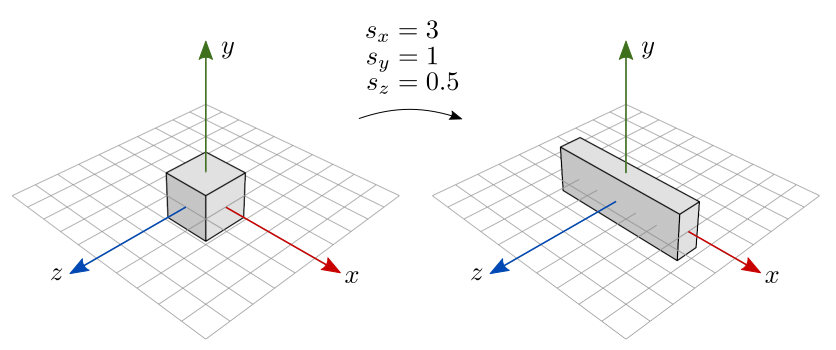
Figura 7.7: Escala não uniforme.
Em resumo, se \(s\) é um fator de escala (\(s_x\), \(s_y\) ou \(s_z\)):
- \(0 \leq s < 1\) faz o objeto diminuir de tamanho na direção correspondente.
- \(s = 1\) mantém o tamanho do objeto.
- \(s > 1\) faz o objeto aumentar de tamanho na direção correspondente.
Se o sinal de \(s\) é negativo, o resultado é uma reflexão na direção correspondente. A figura 7.8 ilustra o resultado da reflexão em \(x\) e \(y\) sem alteração do tamanho do objeto (\(|s|=1\)).
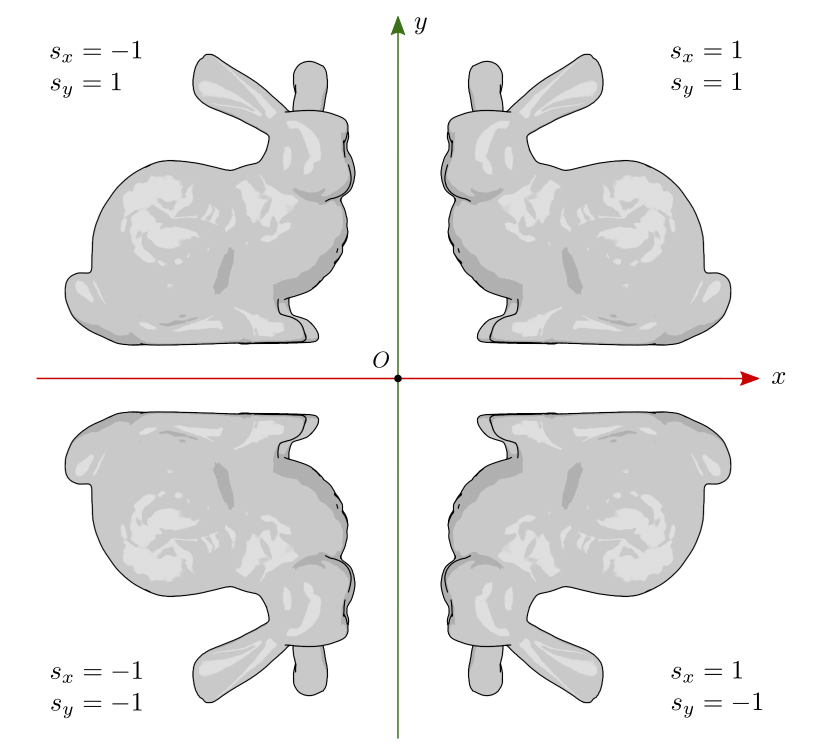
Figura 7.8: Reflexão.
A matriz de escala é definida como
\[ \mathbf{S}=\mathbf{S}(s_x,s_y,s_z)= \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}. \]
Assim,
\[ \mathbf{p}'=\mathbf{S}\mathbf{p} \]
\[ \begin{bmatrix} s_x x\\ s_y y\\ s_z z\\ 1\end{bmatrix} = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1\end{bmatrix}. \]
A inversa é a escala pelo valor recíproco dos fatores de escala:
\[ \mathbf{S}^{-1}(s_x,s_y,s_z) = \mathbf{S}\left(\frac{1}{s_x},\frac{1}{s_y},\frac{1}{s_z}\right) \]
Assim, se um objeto teve seu tamanho dobrado (\(s=2\)), para voltar ao tamanho original devemos diminuir seu tamanho pela metade (\(s=1/2=0.5\)).
Rotação
A rotação é um tipo de transformação linear que produz uma movimentação radial em torno de um ponto ou eixo de rotação. A rotação é uma transformação de corpo rígido, pois não altera as distâncias entre os pontos do objeto rodado.
Para simplificar, vamos primeiramente definir uma rotação no plano cartesiano e depois estender o conceito para o espaço tridimensional.
Um ponto \(P=(x,y)\) é rodado em torno da origem por um ângulo \(\theta\) no sentido anti-horário, resultando em um ponto \(P'=(x',y')\) como mostra a figura 7.9.
Figura 7.9: Rotação no plano.
Podemos determinar a transformação que leva \(P\) a \(P'\) através da representação dos pontos em coordenadas polares:
\[ \begin{align} x &= r \cos \phi,\\ y &= r \sin \phi,\\ \\ x' &= r \cos (\phi + \theta),\\ y' &= r \sin (\phi + \theta).\\ \end{align} \] Usando a soma de cossenos,
\[ \begin{align} x' &= r \cos (\phi + \theta)\\ &= r \cos \phi \cos \theta - r\sin\phi\sin\theta,\\ y' &= r \sin (\phi + \theta)\\ &= r \sin \phi \cos \theta + r\cos\phi\sin\theta. \end{align} \]
Substituindo por \(x\) e \(y\), obtemos o resultado:
\[ \begin{align} x' &= x \cos \theta - y \sin \theta,\\ y' &= y \cos \theta + x \sin \theta. \end{align} \]
Em notação matricial:
\[ \begin{bmatrix} x'\\ y'\end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \phantom{-}\cos \theta \end{bmatrix} \begin{bmatrix} x\\ y\end{bmatrix}. \] A matriz
\[ \mathbf{R}(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \phantom{-}\cos \theta \end{bmatrix} \]
representa a transformação de rotação em torno da origem por um ângulo \(\theta\) no sentido anti-horário.
Rotação 3D
No espaço tridimensional, a rotação ocorre em torno de um eixo de referência.
Vamos derivar as transformações de rotação em torno dos três eixos do sistema de coordenadas cartesiano orientado segundo a regra da mão direita (figura 7.10).
Figura 7.10: Sistema de coordenadas baseado na regra da mão direita.
Um ponto \(P=(x,y,z)\) é rodado em torno do eixo \(z\) por um ângulo \(\theta\) no sentido anti-horário, resultando em um ponto \(P'=(x',y',z')\), como mostra a figura 7.11.
Figura 7.11: Rotação em torno de \(z\).
Pela regra da mão direita, é como se o eixo \(z\) positivo na figura 7.11 estivesse saindo da tela. Assim, as coordenadas \(x\) e \(y\) mudam como na rotação 2D, e a coordenação \(z\) não é modificada:
\[ \begin{align} x' &= x \cos \theta - y \sin \theta,\\ y' &= y \cos \theta + x \sin \theta,\\ z' &= z. \end{align} \]
A figura 7.12 ilustra o resultado da rotação em \(\pi/6\) radianos (\(30^{\circ}\)) em torno do eixo \(z\), aplicada sobre um cubo centralizado na origem. Como o ângulo é positivo, o objeto é rodado no sentido anti-horário.
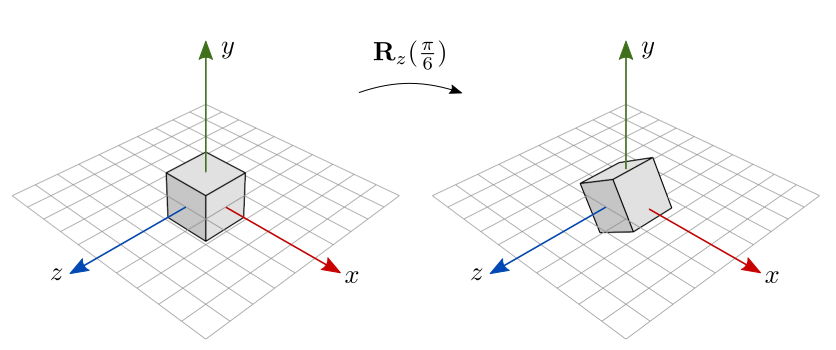
Figura 7.12: Rotação sobre um objeto centralizado na origem.
A figura 7.13 mostra a rotação em \(\pi/6\) radianos em torno do eixo \(z\) sobre um cubo não centralizado na origem. Observe que todos os pontos ao longo do eixo \(z\) permanecem inalterados. De fato, na rotação 3D, todos os pontos ao longo do eixo de rotação são pontos fixos.
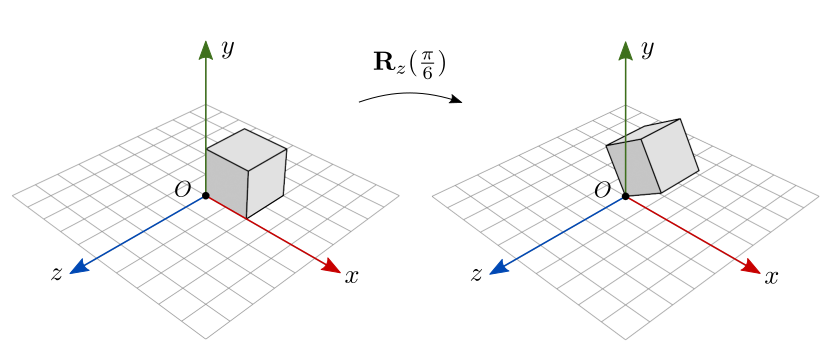
Figura 7.13: Rotação sobre um objeto não centralizado na origem.
Podemos obter a rotação em torno dos outros eixos através da substituição cíclica das coordenadas \(x\), \(y\) e \(z\) nas expressões de rotação em torno de \(z\), segundo a ordem mostrada na figura 7.14.
Figura 7.14: Ordem cíclica de substituição das coordenadas.
Assim, a rotação em torno do eixo \(x\) resultará em:
\[ \begin{align} y' &= y \cos \theta - z \sin \theta,\\ z' &= z \cos \theta + y \sin \theta,\\ x' &= x. \end{align} \]
A rotação em torno do eixo \(y\) é obtida através de mais uma substituição cíclica das coordenadas nas expressões acima:
\[ \begin{align} z' &= z \cos \theta - x \sin \theta,\\ x' &= x \cos \theta + z \sin \theta,\\ y' &= y. \end{align} \]
As matrizes de rotação em torno dos eixos \(x\), \(y\) e \(z\) ficam como a seguir:
\[ \mathbf{R_x}(\theta)= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta & 0 \\ 0 & \sin \theta & \phantom{-}\cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix},\\ \mathbf{R_y}(\theta)= \begin{bmatrix} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix},\\ \mathbf{R_z}(\theta)= \begin{bmatrix} \cos \theta & -\sin \theta & 0 & 0 \\ \sin \theta & \phantom{-}\cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}. \]
A matriz inversa de uma rotação por um ângulo \(\theta\) é simplesmente a matriz de rotação pelo mesmo eixo, mas pelo ângulo \(-\theta\):
\[ \mathbf{R_x}(\theta)^{-1}=\mathbf{R_x}(-\theta),\\ \mathbf{R_y}(\theta)^{-1}=\mathbf{R_y}(-\theta),\\ \mathbf{R_z}(\theta)^{-1}=\mathbf{R_z}(-\theta). \]
Além disso, as matrizes de rotação são matrizes ortogonais. Desse modo, sua inversa é sua transposta:
\[ \mathbf{R_x}(\theta)^{-1}=\mathbf{R_x}(\theta)^T,\\ \mathbf{R_y}(\theta)^{-1}=\mathbf{R_y}(\theta)^T,\\ \mathbf{R_z}(\theta)^{-1}=\mathbf{R_z}(\theta)^T. \]