10.1 Mapeamento

Qualquer função \(f : \mathbb{R}^3 \mapsto \mathbb{R}^2\) que mapeia pontos \((x,y,z)\) do espaço 3D para pontos \((u,v)\) do espaço 2D é uma função de mapeamento de textura. Nesta seção, veremos algumas das funções de mapeamento mais utilizadas: o mapeamento planar, o mapeamento cilíndrico e o mapeamento esférico. Além desses, abordaremos também o mapeamento UV unwrap, também chamado de desdobramento UV, muito utilizado em programas de modelagem 3D e jogos.

Para simplificar, vamos considerar nesta seção que as coordenadas de textura estão restritas ao intervalo \([0,1]\). Entretanto, isso não é uma limitação. Coordenadas fora desse intervalo podem ser tratadas de acordo com as abordagens descritas na seção 10.2.

Mapeamento planar

O mapeamento planar consiste em uma projeção linear e paralela dos pontos do espaço 3D para o plano do espaço de textura 2D. Geralmente a projeção é feita na direção de algum eixo principal do espaço 3D. Por exemplo, um mapeamento planar na direção do eixo \(x\) pode ser definido como:

\[ \begin{align} u&=1-z,\\ v&=y. \end{align} \]

Considere o mapa de textura difusa mostrado na figura 10.2. Usando mapeamento planar na direção de \(x\), um cubo unitário de \((0,0,0)\) a \((1,1,1)\) mapeado com essa textura terá a aparência mostrada na figura 10.3.

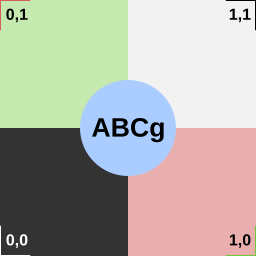
Figura 10.2: Textura difusa com padrão de teste.

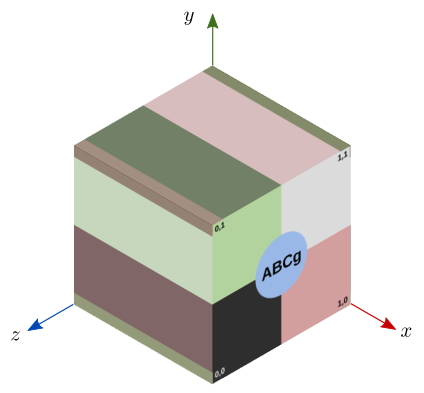
Figura 10.3: Mapeamento planar na direção x sobre um cubo unitário.

Observe como o lado de cima e lado esquerdo do cubo repetem, respectivamente, a cor dos texels com \(v=1\) e \(u=0\) (a mudança de tom é resultado da iluminação). Isso acontece porque todos os pontos ao longo de uma reta na direção \(x\) são mapeados para um mesmo texel.

Um mapeamento planar na direção do eixo \(y\) pode ser definido como:

\[ \begin{align} u&=x,\\ v&=1-z. \end{align} \] A figura 10.4 mostra o resultado desse mapeamento sobre o cubo unitário.

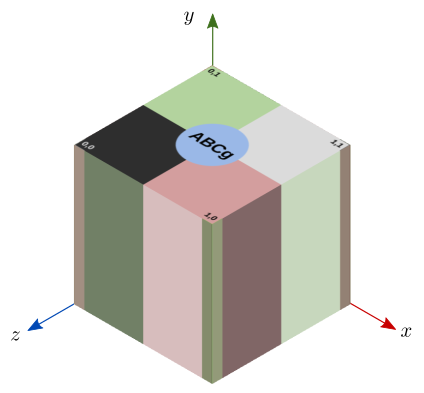
Figura 10.4: Mapeamento planar na direção y sobre um cubo unitário.

Um mapeamento planar na direção do eixo \(z\) pode ser definido como:

\[ \begin{align} u&=x,\\ v&=y. \end{align} \]

A figura 10.5 mostra o resultado desse mapeamento sobre o cubo unitário.

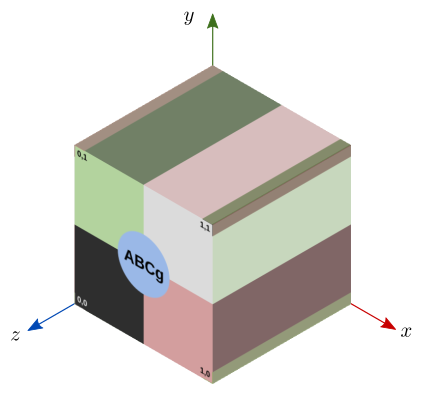
Figura 10.5: Mapeamento planar na direção z sobre um cubo unitário.

Os mapeamentos planares nas direções \(x\), \(y\) e \(z\) podem ser combinados para formar um mapeamento triplanar. A ideia consiste em calcular três pares de coordenadas \((u,v)\), um para cada mapeamento planar,

\[ (u_x,v_x),\qquad(u_y,v_y),\qquad(u_z,v_z), \]

e então combinar o valor dos texels amostrados com essas coordenadas de acordo com um critério. Um critério simples é calcular uma média ponderada dos texels. Os pesos da média podem ser as coordenadas \((n_x, n_y, n_z)\) do vetor normal normalizado, em valor absoluto. Por exemplo, se \(T(u,v)\) é o texel amostrado na posição \((u,v)\) do espaço de textura, a combinação do mapeamento triplanar pode ser calculada como

\[ T(u_x, v_x)|n_x| + T(u_y, v_y)|n_y| + T(u_z, v_z)|n_z|. \]

Na renderização do cubo unitário, o resultado será semelhante ao exibido na figura 10.6.

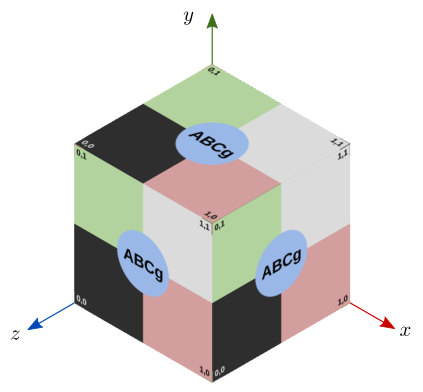
Figura 10.6: Mapeamento triplanar sobre um cubo unitário.

Mapeamento cilíndrico

No mapeamento cilíndrico, a textura é mapeada de tal forma que, se o objeto renderizado é um cilindro unitário alinhado com o eixo \(y\) e com base em \(y=0\), o resultado será equivalente a envolver a área lateral do cilindro com a textura. A figura 10.7 ilustra um exemplo com a visão de frente e de trás do cilindro. Observe como os lados esquerdo (\(u=0\)) e direito (\(u=1\)) da textura se unem na parte de trás do cilindro.

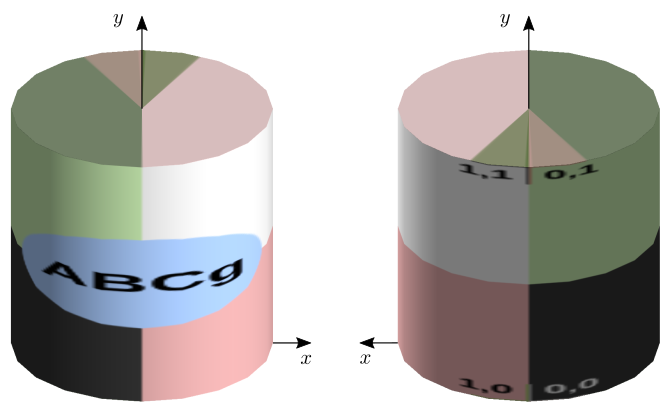
Figura 10.7: Mapeamento cilíndrico em um cilindro unitário.

Seja \(\mathbf{p}=\begin{bmatrix}p_x & p_y & p_z\end{bmatrix}^T\) um ponto do espaço euclidiano. O mapeamento cilíndrico é definido a partir do ângulo \(\theta\) que \(\mathbf{p}\) forma em torno do cilindro alinhado ao eixo \(y\), e a elevação \(p_y\) em relação à altura do cilindro, como mostra a figura 10.8.

Figura 10.8: Geometria do mapeamento cilíndrico.

• O ângulo \(\theta \in [-\pi, \pi]\) é mapeado para \(u \in [0,1]\).
• A altura \(y\) é mapeada diretamente para \(v\), isto é, \(v=p_y\).

Observe que

\[ \tan{\theta}=\frac{p_x}{p_z}. \] Logo,

\[ \theta=\arctan\left({\frac{p_x}{p_z}}\right). \]

O ângulo é calculado corretamente para \(p_z>0\). Entretanto, a imagem da função arco tangente está restrita ao intervalo \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\). Para que \(\theta\) seja um ângulo em um intervalo de 360 graus, precisamos ajustar o intervalo da função arco tangente de acordo com o sinal de \(p_x\) e \(p_z\). Isso pode ser feito através da definição de uma função \(\textrm{arctan2}(p_x, p_z)\), que retorna um ângulo no intervalo \((-\pi, \pi]\):

\[ \operatorname{atan2}(p_x, p_z) = \begin{cases} \arctan\left(\dfrac{p_x}{p_z}\right) &\text{se } p_z > 0, \\ \arctan\left(\dfrac{p_x}{p_z}\right) + \pi &\text{se } p_z < 0 \text{ e } p_x \ge 0, \\ \arctan\left(\dfrac{p_x}{p_z}\right) - \pi &\text{se } p_z < 0 \text{ e } p_x < 0, \\ +\dfrac{\pi}{2} &\text{se } p_z = 0 \text{ e } p_x > 0, \\ -\dfrac{\pi}{2} &\text{se } p_z = 0 \text{ e } p_x < 0, \\ \text{indefinido} &\text{se } p_z = 0 \text{ e } p_x = 0. \end{cases} \]

A função \(\operatorname{atan2}\) está presente nas bibliotecas matemáticas das principais linguagens de programação. Por exemplo, na biblioteca padrão do C++, a função é implementada por std::atan2. Em GLSL, a função é atan e recebe dois parâmetros (a função com um parâmetro é a função arco tangente convencional).

A conversão de \(\theta \in (-\pi, \pi]\) para \(u \in (0,1]\) é obtida com o mapeamento linear:

\[ u = \frac{\theta}{2\pi}+0.5. \]

Logo, o mapeamento cilíndrico é definido como

\[ \begin{align} u&=\frac{\textrm{arctan2}\left(p_x, p_z\right)}{2\pi}+0.5,\\ v&=p_y, \end{align} \]

Mapeamento esférico

No mapeamento esférico, a textura é mapeada de tal forma que, se o objeto renderizado é uma esfera centralizada na origem, o resultado será equivalente a envolver a esfera fazendo com que \(u\) e \(v\) sejam, respectivamente, a longitude e a latitude, como em uma projeção cilíndrica equidistante usada em cartografia:

• Os texels da linha \(v=0\) e \(v=1\) serão mapeados, respectivamente, para o polo sul e polo norte da esfera no eixo \(y\);
• Os texels com \(v=0.5\) serão mapeados para o equador da esfera no plano \(y=0\);
• Os texels com \(u=0\) e \(u=1\) serão mapeados para o meridiano central no plano \(yz\) com \(z<0\).

A figura 10.9 mostra um exemplo de esfera texturizada com mapeamento esférico, visto de frente e de cima (polo norte).

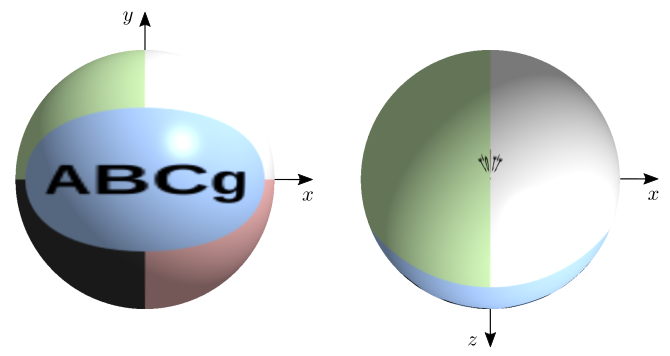
Figura 10.9: Mapeamento esférico em uma esfera unitária.

Seja \(\mathbf{p}=\begin{bmatrix}p_x & p_y & p_z\end{bmatrix}^T\) um ponto do espaço euclidiano. O mapeamento cilíndrico é definido a partir do ângulo \(\theta\) (longitude) e \(\phi\) (latitude) da esfera que contém \(\mathbf{p}\), como mostra a geometria da figura 10.10.

Figura 10.10: Geometria do mapeamento esférico.

A coordenada \(u\) é calculada como no mapeamento cilíndrico:

\[ u=\frac{\textrm{arctan2}\left(p_x, p_z\right)}{2\pi}+0.5. \]

Para determinar \(v\), observe, na figura 10.10, que

\[ \begin{align} \sin \phi = \frac{p_y}{|\mathbf{p}|}.\\ \end{align} \]

Logo,

\[ \phi = \arcsin \left( \frac{p_y}{|\mathbf{p}|} \right), \]

onde

\[ |\mathbf{p}|=\sqrt{x^2+y^2+z^2}. \]

A conversão de \(\phi \in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) para \(v \in (0,1]\) é obtida com o mapeamento linear:

\[ v = \frac{\phi}{\pi}+0.5. \]

Logo, o mapeamento esférico é definido como

\[ \begin{align} u&=\frac{\textrm{arctan2}\left(p_x, p_z\right)}{2\pi}+0.5,\\ v&=\frac{\arcsin\left(\dfrac{p_y}{|\mathbf{p}|}\right)}{\pi}+0.5, \end{align} \]

Mapeamento UV unwrap

No lugar de usar as funções anteriores de mapeamento de textura, podemos definir diretamente quais são as coordenadas \((u,v)\) de cada vértice da malha geométrica. Isso pode ser feito através da inclusão de um atributo adicional de vértice, de forma semelhante como fizemos para a definição de cores nos vértices ou normais de vértices. Durante a rasterização, as coordenadas de textura definidas nos vértices são interpoladas para cada fragmento da primitiva. Assim, cada fragmento terá coordenadas de textura interpoladas e a textura pode então ser amostrada no fragment shader.

Para determinar as coordenadas \((u,v)\) de cada vértice de uma malha poligonal, técnicas de modelagem geométrica podem ser utilizadas para “desdobrar” a malha sobre o plano da textura, em um processo chamado de UV unwrap ou desdobramento UV.

A figura 10.11 mostra um exemplo de objeto 3D renderizado com mapeamento UV unwrap. O objeto é uma lâmpada à óleo romana do acervo do Museu Britânico. O modelo original tem 500 mil triângulos e foi adquirido por um scanner 3D. Aqui, o modelo exibido tem apenas 10 mil triângulos para facilitar a visualização do mapeamento no sistema de coordenadas de textura. Observe, no mapa UV, como a malha é recortada em diferentes pedaços para ser desdobrada sem sobreposições sobre o plano. O mapeamento procura manter a proporção entre a área dos polígonos originais de modo que a densidade dos texels amostrados na superfície seja a mais uniforme possível.

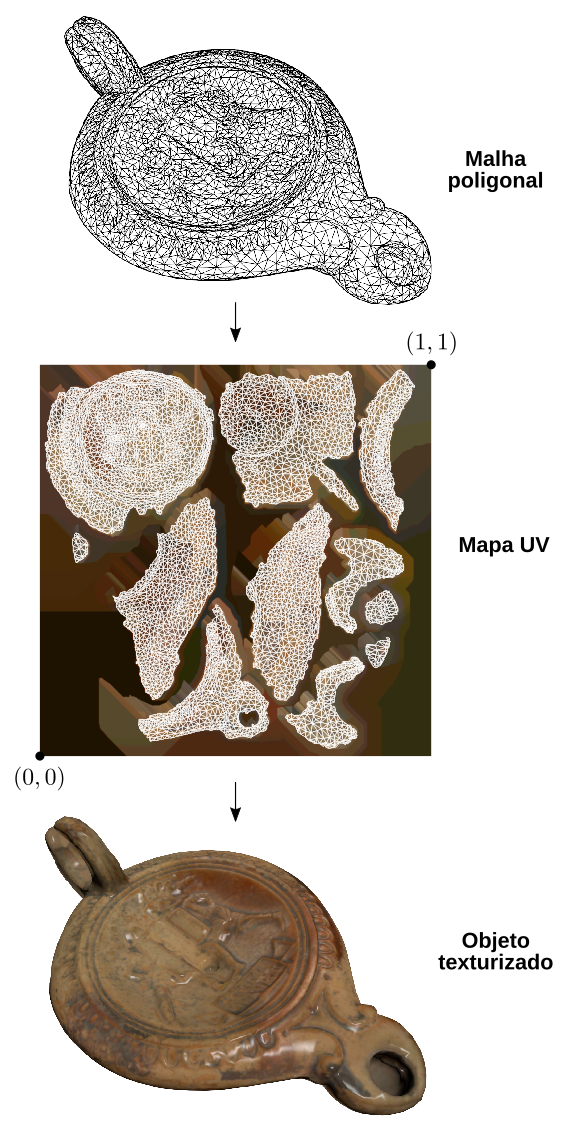
Figura 10.11: Mapeamento UV.

Como referência, a figura 10.12 mostra o mapa de textura utilizado e o objeto sem texturização.

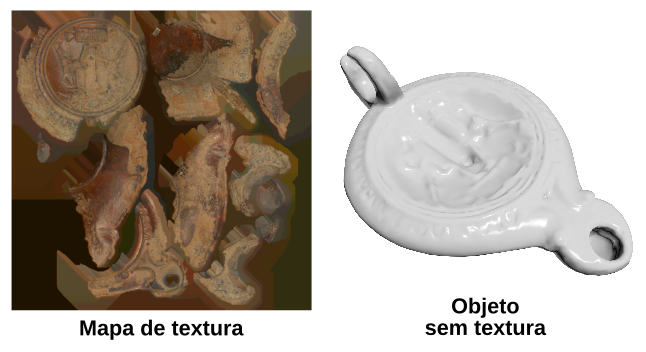
Figura 10.12: Mapa de textura da lâmpada romana, e objeto sem textura.

O desdobramento UV é a técnica mais utilizada de mapeamento de texturas em programas de modelagem e renderização, como o Blender. O formato OBJ suporta modelos com coordenadas de textura por vértice definidas através de desdobramento UV.