9.3 Modelo de Blinn–Phong
O modelo de Blinn–Phong (Blinn 1977) é uma modificação do modelo de reflexão de Phong. A reflexão especular \(\mathbf{I}_s\) para uma fonte de luz é calculada como
\[ \mathbf{I}_s=\kappa_s \iota_{s}(\hat{\mathbf{n}} \cdot \hat{\mathbf{h}})^\alpha, \]
onde
\[ \hat{\mathbf{h}}=\frac{\hat{\mathbf{l}} + \hat{\mathbf{v}}}{|\hat{\mathbf{l}} + \hat{\mathbf{v}}|}. \]
O vetor \(\hat{\mathbf{h}}\) é chamado de halfway vector e está na metade do caminho entre os vetores \(\hat{\mathbf{l}}\) e \(\hat{\mathbf{v}}\) (figura 9.17).
Figura 9.17: Geometria do halfway vector.
Ao usar o cosseno do ângulo entre \(\hat{\mathbf{n}}\) e \(\hat{\mathbf{h}}\) no lugar do cosseno do ângulo entre \(\hat{\mathbf{r}}\) e \(\hat{\mathbf{v}}\), o modelo de Blinn-Phong consegue reproduzir melhor o comportamento da reflexão especular.
No modelo de Phong, o brilho especular é sempre redondo em uma superfície plana. No modelo de Blinn–Phong, o brilho especular é redondo quando a superfície é vista de frente, e alongado verticalmente quando a direção de visão e a direção à fonte de luz estão rentes à superfície. A figura 9.18 compara o formato do brilho especular sobre o lado plano de um objeto visto nessa configuração.
No mundo real, o alongamento do brilho especular pode ser observado, por exemplo, no brilho da luz do sol sobre o mar quando o sol está próximo do horizonte, ou no reflexo da luz sobre um chão molhado, quando a luz é gerada por um poste distante ou pelos faróis de um carro.

Figura 9.18: Diferença entre o formato do brilho especular nos modelos de Phong e Blinn–Phong.
O modelo de Blinn–Phong também pode ser mais eficiente que o modelo de Phong. Se a projeção utilizada for ortográfica e a fonte de luz estiver infinitamente longe do objeto iluminado (como na fonte de luz direcional), então \(\hat{\mathbf{h}}\) só precisa ser calculado uma vez e pode ser reutilizado para todos os pontos do objeto. O vetor só precisa ser atualizado se a direção de visão ou a direção da fonte de luz for modificada.
A possibilidade de otimização do modelo de Blinn–Phong é pouco explorada atualmente, uma vez que a maior parte das aplicações usa projeção perspectiva ou usa câmeras ou fontes de luz dinâmicas. Entretanto, esse aspecto foi uma vantagem importante nos limitados sistemas gráficos da década de 1980 e início da década de 1990.
A equação completa do modelo de Blinn–Phong é a seguinte:
\[ \mathbf{I}=\kappa_a \iota_a + \sum_{i=1}^m \left(\kappa_d \iota_{d_i} (\hat{\mathbf{l}}_i \cdot \hat{\mathbf{n}}) + \kappa_s \iota_{s_i} (\hat{\mathbf{n}} \cdot \hat{\mathbf{h}})^\alpha\right), \] As constantes utilizadas são as mesmas do modelo de Phong. Entretanto, um mesmo valor da constante \(\alpha\) produzirá um brilho especular maior no modelo de Blinn–Phong, como mostra a figura 9.19. Essa alteração do brilho pode ser compensada aumentando o valor da constante.
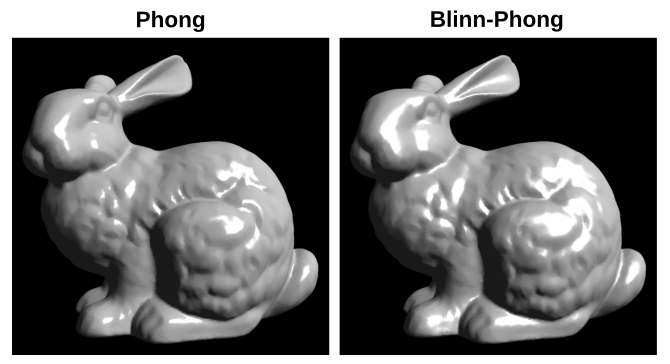
Figura 9.19: Tamanho do brilho especular nos modelos de Phong e Blinn–Phong usando o mesmo expoente de brilho.
Pela sua simplicidade e melhor fidelidade de reprodução de brilhos especulares, o modelo de Blinn–Phong é mais utilizado que o modelo de Phong em síntese de imagens em tempo real.