7.5 Espaços do OpenGL

Vimos que, no pipeline gráfico do OpenGL, as primitivas só são renderizadas se estiverem contidas em um “volume de visão” formado por um cubo centralizado na origem, com coordenadas que vão de \(-1\) a \(1\). As coordenadas desse espaço tridimensional são chamadas de coordenadas normalizadas do dispositivo, ou NDC (figura 7.15).

Volume de visão em coordenadas normalizadas do dispositivo.

Figura 7.15: Volume de visão em coordenadas normalizadas do dispositivo.

Observe que os eixos do NDC seguem a regra da mão esquerda, isto é, o eixo \(z\) positivo aponta para dentro da tela.

Por uma questão de simplicidade, até agora representamos todos os objetos diretamente no NDC. Entretanto, essa abordagem é pouco flexível para a maioria das aplicações. Com frequência precisamos trabalhar com coordenadas em intervalos maiores em um sistema orientado segundo a regra da mão direita.

Felizmente, podemos representar mudanças de pontos entre diferentes espaços intermediários através de transformações matriciais, da forma que considerarmos mais conveniente. Só precisamos garantir que, no vertex shader, essas coordenadas serão finalmente mapeadas para o espaço homogêneo de recorte, que é o sistema de coordenadas utilizado na variável embutida gl_Position, ou diretamente para o NDC, fazendo com que a coordenada homogênea (\(w\)) seja sempre 1.

Usaremos os seguintes sistemas de coordenadas, nessa ordem:

  1. Espaço do objeto (local space ou object space).
  2. Espaço do mundo (world space).
  3. Espaço da câmera (view space, camera space ou eye space).

Além desses, há os espaços utilizados durante o processamento do pipeline gráfico do OpenGL:

  1. Espaço de recorte (clip space).
  2. Espaço normalizado do dispositivo (NDC space).
  3. Espaço da janela (window space).

Um modelo 3D está inicialmente no espaço do objeto. Esse é o espaço das coordenadas dos atributos dos vértices armazenados no VBO. No pipeline de renderização, os pontos/vetores do espaço local são convertidos para os espaços subsequentes através de multiplicações com matrizes de transformação (matrizes \(4 \times 4\), como visto na seção anterior). A figura 7.16 mostra a sequência de transformações de pontos/vetores, do espaço do objeto ao espaço da janela.

Etapas de transformação entre sistemas de coordenadas no pipeline gráfico.

Figura 7.16: Etapas de transformação entre sistemas de coordenadas no pipeline gráfico.

Nesta seção, serão abordados apenas os três primeiros espaços, que são os espaços definidos pelo usuário:

  • Espaço do objeto;
  • Espaço do mundo;
  • Espaço da câmera.

Os espaços restantes serão detalhados no próximo capítulo.

Espaço do objeto

É o espaço local utilizado na definição do modelo geométrico original. Por exemplo, o modelo “Stanford Bunny” do arquivo bunny.obj (seção 6.4) foi definido em um sistema de coordenadas que segue a regra da mão direita (RHS, de right-handed coordinate system), sendo que o eixo \(y\) positivo aponta para cima (figura 7.17). A origem desse sistema de coordenadas é o centro da base do coelho. Além disso, as coordenadas do modelo estão na faixa \(x \in [-1, 0.7]\), \(y \in [0, 1.6]\), \(z \in [-0.5, 0.7]\).

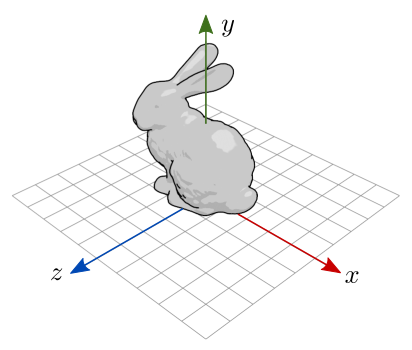
Espaço do objeto do modelo do arquivo `bunny.obj`.

Figura 7.17: Espaço do objeto do modelo do arquivo bunny.obj.

O cubo definido no arquivo box.obj (seção 6.4) usa um sistema de coordenadas que segue a regra da mão esquerda (LHS, de left-handed coordinate system). A origem é o centro do cubo e as coordenadas variam de \(-0.5\) a \(0.5\) em cada dimensão.

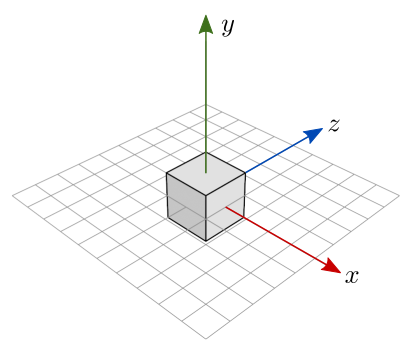
Espaço do objeto do modelo do arquivo `box.obj`.

Figura 7.18: Espaço do objeto do modelo do arquivo box.obj.


Observação

Um triângulo definido em um espaço RHS tem sua orientação invertida quando renderizado sem modificações em um espaço LHS, como o NDC.

No espaço RHS, o lado da frente de um triângulo no plano \(xy\) é o lado com orientação CCW para um observador olhando na direção de \(z\) negativo. Entretanto, se esse mesmo triângulo é utilizado sem modificação no NDC, o lado da frente ficará orientado no sentido CW após o mapeamento no espaço da janela, como se o observador agora olhasse na direção de \(z\) negativo do espaço LHS (figura 7.19).

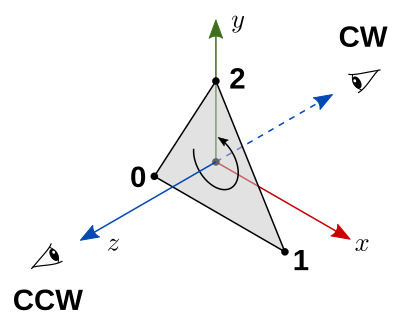
Mudança de orientação de um sistema RHS para LHS.

Figura 7.19: Mudança de orientação de um sistema RHS para LHS.

Esse problema pode ser resolvido facilmente através da negação de cada coordenada \(z\) do modelo. Faremos isso na matriz de projeção, pois sempre consideraremos que o espaço do objeto é RHS.

Espaço do mundo

O espaço do mundo é o frame utilizado para dispor os diferentes objetos em um cenário virtual. A origem do espaço do mundo pode ser um ponto que indica o centro do cenário, a posição inicial de um personagem virtual, ou simplesmente um ponto arbitrário no espaço.

Em nossas aplicações, adotaremos como convenção que o espaço do mundo é um espaço euclidiano tridimensional RHS, sendo que o eixo \(x\) positivo aponta para o lado, e o eixo \(y\) positivo aponta para cima. O “chão” pode ser considerado como o plano \(xz\) com altura \(y=0\). A figura 7.20 ilustra a composição de uma cena através da disposição de objetos sobre o plano \(y=0\) do espaço do mundo.

Cena no espaço do mundo.

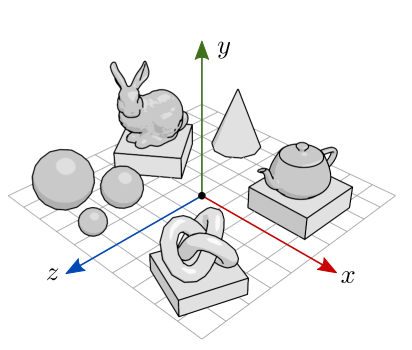
Figura 7.20: Cena no espaço do mundo.

Em uma cena composta por vários objetos, a transformação que posiciona e orienta um objeto na cena é definida através de uma matriz de modelo (model matrix).

A matriz de modelo é uma concatenação de transformações de rotação, escala e translação que representa uma mudança de frame: do espaço do objeto para o espaço do mundo.

Cada objeto de uma cena deve ter a sua própria matriz de modelo.

Na cena da figura 7.20, as bases cuboides compartilham o mesmo modelo de um cubo mostrado na figura 7.21, mas cada um usa uma matriz de modelo diferente, pois cada cuboide está numa posição/orientação/escala diferente na cena.

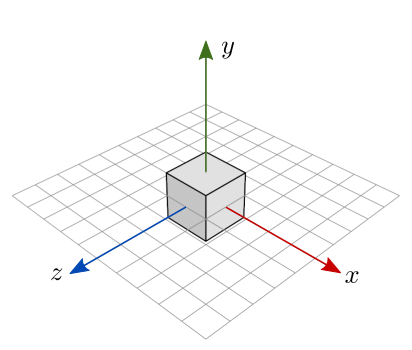
Cubo unitário centralizado na origem.

Figura 7.21: Cubo unitário centralizado na origem.

Por exemplo, para o objeto cuboide que serve de base para o coelho, a matriz de modelo é a seguinte concatenação de transformações:

\[\mathbf{M}=\mathbf{T}\left(-3,\frac{1}{2},-\frac{1}{2}\right).\mathbf{R}_y\left(\frac{7\pi}{36}\right).\mathbf{S}\left(\frac{5}{4}, \frac{1}{2}, \frac{5}{4}\right). \]

A matriz representa a aplicação das transformações na ordem de leitura da direita para a esquerda (figura 7.22):

  1. Escala de \(s_x=1.25\), \(s_y=0.5\), \(s_z=1.25\);
  2. Rotação por \(7\pi/36\) radianos (\(35^{\circ}\)) em torno de \(y\);
  3. Translação por \(t_x=-3\), \(t_y=0.5\), \(t_z=-0.5\).
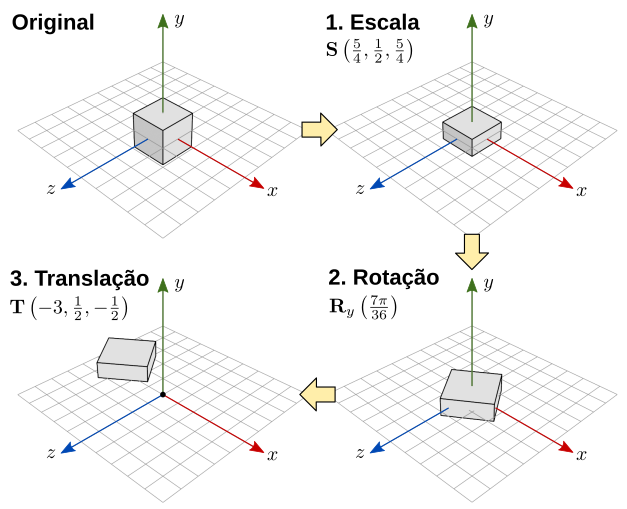
Sequência de transformações de uma matriz de modelo.

Figura 7.22: Sequência de transformações de uma matriz de modelo.

Se a matriz de modelo é a matriz que converte pontos no frame local para pontos no frame do mundo, então a inversa da matriz de modelo faz o mapeamento inverso, isto é, do frame do mundo para o frame local. No caso da base cuboide, essa transformação inversa é

\[ \begin{align} \mathbf{M}^{-1}&=\left(\mathbf{T}\left(-3,\frac{1}{2},-\frac{1}{2}\right).\mathbf{R}_y\left(\frac{7\pi}{36}\right).\mathbf{S}\left(\frac{5}{4}, \frac{1}{2}, \frac{5}{4}\right)\right)^{-1}\\ &=\mathbf{S}\left(\frac{5}{4}, \frac{1}{2}, \frac{5}{4}\right)^{-1}.\mathbf{R}_y\left(\frac{7\pi}{36}\right)^{-1}.\mathbf{T}\left(-3,\frac{1}{2},-\frac{1}{2}\right)^{-1}\\ &=\mathbf{S}\left(\frac{4}{5}, 2, \frac{4}{5}\right).\mathbf{R}_y\left(-\frac{7\pi}{36}\right).\mathbf{T}\left(3,-\frac{1}{2},\frac{1}{2}\right). \end{align} \]

Note que as transformações concatenadas da matriz inversa desfazem cada uma das transformações da figura 7.22, no sentido contrário (da etapa 3 até o modelo original).

Espaço da câmera

O espaço da câmera representa o ponto de vista da câmera virtual posicionada no mundo, isto é, o ponto de vista de um observador em primeira pessoa dentro da cena.

No espaço da câmera, a câmera está posicionada na origem, olhando na direção do eixo \(z\) negativo. As coordenadas de todos os objetos da cena são descritos em relação à câmera. A figura 7.23 ilustra o frame de uma câmera em relação ao mundo. A direção de visão é representada pela seta tracejada, que é a direção do eixo \(z\) negativo do frame da câmera.

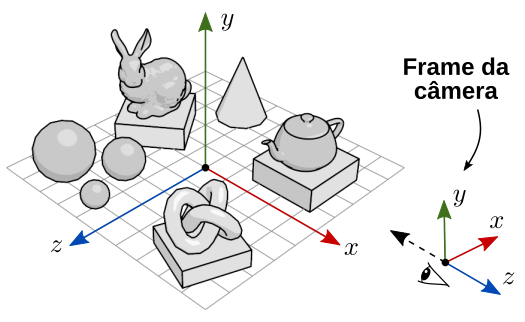
Frame da câmera em relação ao frame do mundo.

Figura 7.23: Frame da câmera em relação ao frame do mundo.

A figura 7.24 ilustra como a cena é vista a partir da câmera, e como a câmera vê o frame do mundo.

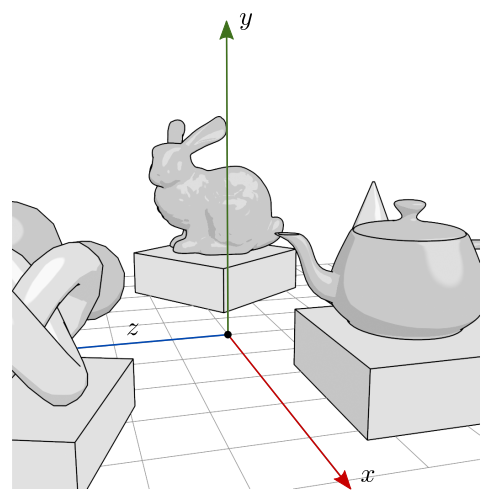
Frame do mundo do ponto de vista da câmera.

Figura 7.24: Frame do mundo do ponto de vista da câmera.

A transformação que transforma pontos do espaço do mundo para o espaço da câmera é definida através de uma matriz de visão (view matrix). Essa matriz é uma concatenação de rotações e uma translação.

Para construir uma matriz de visão, precisamos de uma posição e uma orientação.

  • A posição é a localização da câmera no espaço do mundo. Do ponto de vista da câmera, é a origem (ponto \((0,0,0)\)) de seu frame. Essa informação fica armazenada na parte de translação da matriz de visão (parte \(3 \times 1\) da quarta coluna)
  • A orientação é uma base ortonormal, e corresponde à parte \(3 \times 3\) superior da matriz de visão (mudança de base).

Descreveremos na seção 7.6 o processo de construção de uma matriz de visão a partir da posição da câmera, a posição para onde a câmera está olhando, e um vetor de direção para cima, que geralmente é o vetor \(\hat{\mathbf{j}}=\begin{bmatrix}0&1&0\end{bmatrix}^T\) do \(\mathbb{R}^3\).

Concatenação das matrizes de modelo e visão

Sempre que um objeto for renderizado, a posição de cada um de seus vértices precisa ser transformada. Isso pode ser feito em duas etapas:

  1. Conversão do espaço local para o espaço do mundo: \[\mathbf{p}'=\mathbf{M}_{\textrm{model}}.\mathbf{p},\] onde \(\mathbf{M}_{\textrm{model}}\) é a matriz de modelo do objeto que está sendo renderizado.

  2. Conversão do espaço do mundo para o espaço da câmera: \[\mathbf{p}''=\mathbf{M}_{\textrm{view}}.\mathbf{p}',\] onde \(\mathbf{M}_{\textrm{view}}\) é a matriz de visão. A matriz de visão deve ser a mesma para todos os objetos da cena renderizada.

É comum combinar as duas transformações em uma só matriz modelo-visão:

\[ \mathbf{M}_{\textrm{modelview}}=\mathbf{M}_{\textrm{view}}.\mathbf{M}_{\textrm{model}}. \]

Assim, no vertex shader basta uma multiplicação matricial para transformar a posição do vértice pela matriz modelo-visão. O resultado será um ponto no espaço da câmera.

Observação

Após a transformação do ponto para o espaço da câmera, é necessário aplicar ainda uma transformação projetiva através de uma matriz de projeção \(\mathbf{M}_{\textrm{proj}}\).

A matriz de projeção converte um ponto do espaço da câmera para o espaço homogêneo de recorte, que é o espaço esperado pela variável embutida gl_Position no vertex shader. A transformação completa fica como a seguir:

\[ \mathbf{p}'=\mathbf{M}_{\textrm{proj}}.\mathbf{M}_{\textrm{view}}.\mathbf{M}_{\textrm{model}}.\mathbf{p}, \]

onde

  • \(\mathbf{p}\) é a entrada do vertex shader, isto é, a posição do vértice no formato \(\begin{bmatrix}x&y&z&1\end{bmatrix}^T\);
  • \(\mathbf{p}'\) é a posição transformada no formato \(\begin{bmatrix}x'&y'&z'&w\end{bmatrix}^T\). Essa é a posição que será copiada para gl_Position.

Os conceitos sobre transformações de projeção e o processo de construir a matriz \(\mathbf{M}_{\textrm{proj}}\) serão abordados no próximo capítulo.