7.6 Câmera LookAt

Câmera LookAt é o nome dado ao frame de câmera virtual {Peye,ˆu,ˆv,ˆn} construído a partir das seguintes informações:

1. Um ponto Peye que corresponde à posição da câmera no espaço do mundo;
2. Um ponto Pat que corresponde à posição aonde a câmera está olhando, também no espaço do mundo²⁸.
3. Um vetor vup utilizado para indicar a direção “para cima” da câmera. Geralmente esse vetor é a direção (0,1,0).

A figura 7.25 ilustra esses elementos, incluindo os vetores {ˆu,ˆv,ˆn} que formam a base ortonormal da câmera.

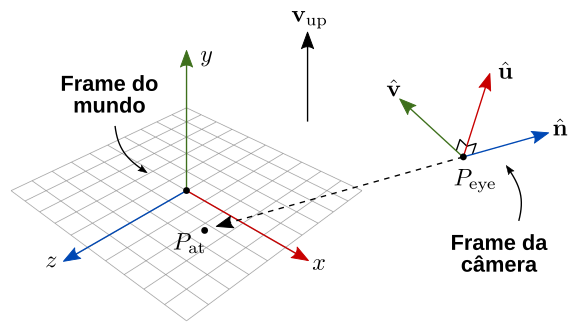
Figura 7.25: Frame da câmera, representado em relação ao mundo.

O sistema de coordenadas da câmera segue a regra da mão direita. Note que a câmera está olhando na direção −ˆn no espaço do mundo, que corresponde à direção do eixo z negativo da câmera.

Inicialmente, não temos a base ortonormal {ˆu,ˆv,ˆn}. Só temos as seguintes informações (ilustradas na figura 7.26):

• A posição da câmera, Peye;
• A posição para onde a câmera deve ser direcionada, Pat;
• O vetor vup, que vamos considerar como sendo o vetor (0,1,0).

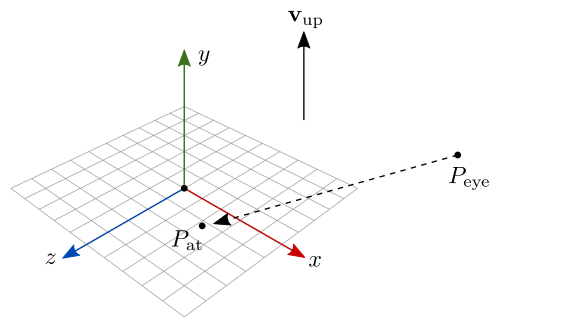
Figura 7.26: Parâmetros de uma câmera LookAt.

Através dessas informações construiremos a base {ˆu,ˆv,ˆn}. Com a base e o ponto de referência (Peye) temos o frame completo para criar a matriz de visão Mview. Como vimos anteriormente, a matriz de visão representa uma mudança de frame: do espaço do mundo para o espaço da câmera.

Construindo o vetor n

Para construir a base ortonormal, primeiro fazemos Peye−Pat para obter o vetor que aponta na direção contrária da direção de visão. Esse vetor é então normalizado para obter ˆn (figura 7.27):

ˆn=Peye−Pat|Peye−Pat|.

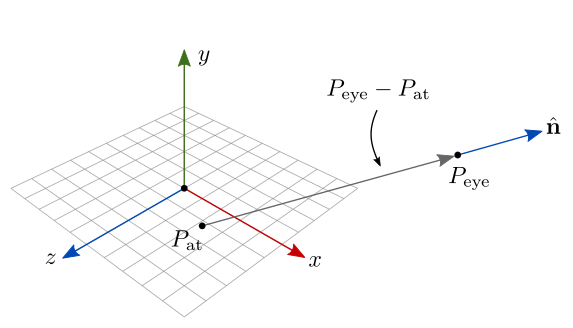
Figura 7.27: Construção do vetor n da câmera LookAt.

Note que ˆn está sendo representado em coordenadas do espaço do mundo. Em relação à câmera, ˆn torna-se o vetor ˆk=(0,0,1), isto é, a direção do eixo z positivo da câmera (direção para trás da câmera).

Construindo o vetor u

Agora que temos ˆn, o segundo passo é calcular o produto vetorial vup׈n e normalizar o resultado. Com isso obtemos o vetor ˆu perpendicular ao plano formado por vup e ˆn (figura 7.28):

ˆu=vup׈n|vup׈n|.

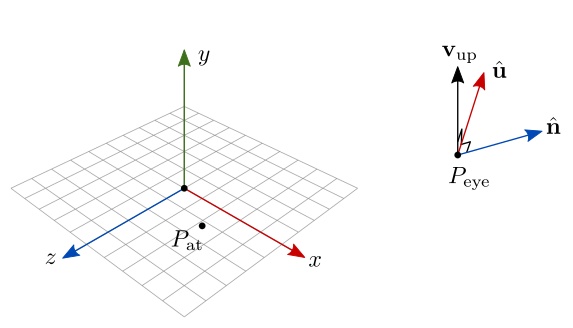
Figura 7.28: Construção do vetor u da câmera LookAt.

No frame da câmera, ˆu corresponde ao vetor ˆi=(1,0,0), isto é, a direção do eixo x da câmera (direção à direita).

Construindo o vetor v

Embora ˆu seja perpendicular a ˆn e a vup, ainda não temos uma base ortonormal pois vup não é necessariamente perpendicular a ˆn. Na figura 7.28, vup e ˆn formam um ângulo menor que 90∘.

Para obter um vetor que seja mutuamente ortogonal a ˆn e ˆu, basta calcularmos o produto vetorial ˆn׈u. O resultado é ˆv (figura 7.29) que já está normalizado pois ˆn e ˆu também têm comprimento 1.

ˆv=ˆn׈u.

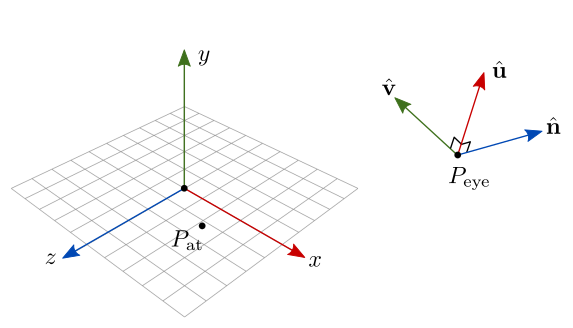
Figura 7.29: Construção do vetor v da câmera LookAt.

Note que, em relação à câmera, ˆv corresponde ao vetor ˆj=(0,1,0), isto é, o eixo y da câmera (direção para cima).

Os vetores {ˆu,ˆv,ˆn} formam a base ortonormal da câmera, representados em relação ao espaço do mundo.

Construindo a matriz de visão

Para a construção da matriz de mudança de frame, vamos relembrar primeiro a matriz de mudança de base.

A matriz com colunas formadas pelos vetores {T(ˆi),T(ˆj),T(ˆk)} representa uma mudança da base {ˆi,ˆj,ˆk} para a base transformada. A transformação T é uma composição de rotações (por exemplo, RzRyRx), que tem o efeito de rodar a base original para a nova.

O que temos atualmente é a base {ˆu,ˆv,ˆn}. Esses vetores estão representados em relação ao espaço do mundo. Se estivessem representados em relação ao espaço da câmera, a base seria {ˆi,ˆj,ˆk}. Então, se construirmos a matriz R de mudança de base,

R=[u11v12n130u21v22n230u31v32n3300001], tal matriz representa a mudança do espaço da câmera para o espaço do mundo. Não é bem o que queremos. Gostaríamos da matriz que faz a transformação inversa, isto é, que converte coordenadas do mundo para a câmera. Entretanto, vamos prosseguir com R da forma como está. Ao final poderemos calcular a matriz inversa da transformação completa, para finalmente obter Mview.

Com a matriz R, a base {ˆi,ˆj,ˆk} no espaço da câmera é transformada por rotações para resultar na base {ˆu,ˆv,ˆn} representada no espaço do mundo. Isso é ilustrado na figura 7.30.

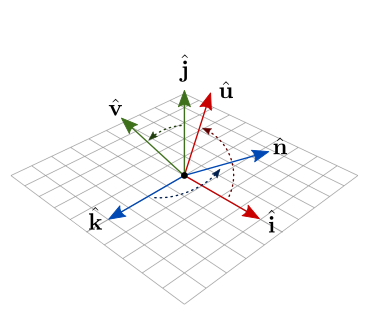
Figura 7.30: Rotação da base representada no espaço da câmera, para a base representada no espaço do mundo.

Além da base, um frame também precisa de um ponto de referência. Esse ponto de referência é o próprio Peye, que representa a origem O no espaço da câmera. Peye é o deslocamento necessário para mover a origem do espaço da câmera para sua posição no espaço do mundo. Em outras palavras, temos uma transformação de translação que pode ser representada pela matriz

T=[100Peyex010Peyey001Peyez0001].

Fazendo a composição das transformações, temos

M=TR M=[100Peyex010Peyey001Peyez0001][u11v12n130u21v22n230u31v32n3300001]. A figura 7.31 ilustra como a matriz de transformação M converte coordenadas do espaço da câmera para o espaço do mundo, que é o equivalente a rodar a base {ˆi,ˆj,ˆk} para {ˆu,ˆv,ˆn} (matriz de rotação R), e então transladar a origem O para Peye (matriz de translação T).

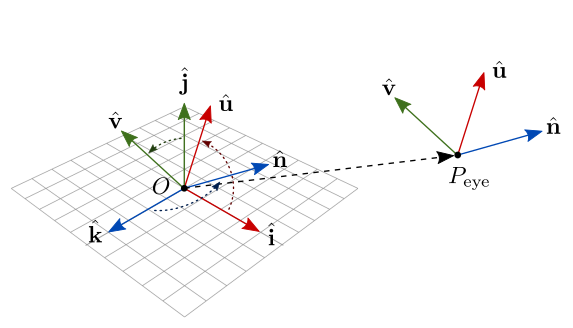
Figura 7.31: Mudança do espaço da câmera para o espaço do mundo.

Para obter Mview, basta calcularmos a inversa de M. Lembre-se que a inversa de uma matriz de rotação é a sua transposta, e a inversa da translação por Peye é a translação por −Peye. Portanto,

Mview=M−1=(TR)−1=([100Peyex010Peyey001Peyez0001][u11v12n130u21v22n230u31v32n3300001])−1=[u11v12n130u21v22n230u31v32n3300001]−1[100Peyex010Peyey001Peyez0001]−1=[u11u21u230v12v22v330n13v23n3300001][100−Peyex010−Peyey001−Peyez0001]=[u11u21u23−ˆu⋅Peyev12v22v33−ˆv⋅Peyen13v23n33−ˆn⋅Peye0001].

A biblioteca GLM possui a função glm::lookAt, definida em cabeçalho glm/gtc/matrix_transform.hpp:

glm::mat4 glm::lookAt(glm::vec3 const& eye, glm::vec3 const& center, glm::vec3 const& up);
glm::dmat4 glm::lookAt(glm::dvec3 const& eye, glm::dvec3 const& center, glm::dvec3 const& up);

glm::lookAt gera a matriz Mview de uma câmera LookAt, dados os parâmetros Peye (eye), Pat (center) e vup (up).

Internamente, a função chama glm::lookAtRH para gerar o frame baseado na regra da mão direita. O conteúdo dessa função é dado a seguir:

template<typename T, qualifier Q>
GLM_FUNC_QUALIFIER mat<4, 4, T, Q> lookAtRH(vec<3, T, Q> const& eye, vec<3, T, Q> const& center, vec<3, T, Q> const& up)
{
    vec<3, T, Q> const f(normalize(center - eye));
    vec<3, T, Q> const s(normalize(cross(f, up)));
    vec<3, T, Q> const u(cross(s, f));

    mat<4, 4, T, Q> Result(1);
    Result[0][0] = s.x;
    Result[1][0] = s.y;
    Result[2][0] = s.z;
    Result[0][1] = u.x;
    Result[1][1] = u.y;
    Result[2][1] = u.z;
    Result[0][2] =-f.x;
    Result[1][2] =-f.y;
    Result[2][2] =-f.z;
    Result[3][0] =-dot(s, eye);
    Result[3][1] =-dot(u, eye);
    Result[3][2] = dot(f, eye);
    return Result;
}

Na linha 4, f (vetor “forward”) é equivalente ao nosso −ˆn.

Na linha 5, s (vetor “side”) é o nosso vetor ˆu, calculado como −ˆn×vup, que é o mesmo que vup׈n, seguido de uma normalização.

Na linha 6, u é o nosso vetor ˆv, calculado como ˆu×−ˆn, que é o mesmo que ˆn׈u.

Nas linhas 9 a 21 é montada a matriz Result, que é a matriz Mview. Internamente, a GLM armazena as matrizes no formato column-major, o que significa que o primeiro índice é a coluna, e o segundo índice é a linha. Levando isso em consideração, observe que a matriz resultante é de fato:

Mview=[u11u21u23−ˆu⋅Peyev12v22v33−ˆv⋅Peyen13v23n33−ˆn⋅Peye0001].

---

28. O ponto “at” também é chamado de “center” ou “target.”↩︎