7 Operações Morfológicas

A morfologia matemática consiste em uma metodologia para análise de imagens que permite a construção de operadores úteis para a descrição de objetos em imagens. A teoria de morfologia matemática foi formulada na década de 1960, por Georges Matheron, Jean Serra e seus colaboradores da Escola Nacional Superior de Minas de Paris, França. Originalmente desenvolvida para manipular imagens binárias, a morfologia matemática foi posteriormente estendida para tratar imagens em níveis de cinza.

Os operadores morfológicos podem ser utilizados em um grande número de aplicações em processamento e análise de imagens, incluindo a extração de componentes conexos, busca de padrões na imagem, extração, destaque e afinamento de bordas dos objetos.

A análise de imagens por meio de operadores morfológicos tem aplicações nos mais diversos domínios do conhecimento, desde aplicações médicas e científicas, como em aplicações industriais.

A morfologia matemática utiliza a teoria de conjuntos para representar a forma dos objetos em uma imagem. Por convenção, objetos em uma imagem binária serão representados por pixels pretos (valor 1), enquanto o fundo é formado por pixels brancos (valor 0). Dessa forma, uma imagem binária pode ser considerada uma coleção de coordenadas discretas que correspondem aos pontos pertencentes aos objetos na imagem.

Nessa representação binária, o conjunto de pixels que definem um objeto pode ser definido como coordenadas $(x,y)$ no espaço bidimensional dos números inteiros. Sendo assim, a imagem abaixo pode ser representada como o seguinte conjunto de coordenadas: $(0;1);(1;0);(1;2);(2;1);(3;0);(4;2);(5;4)$.

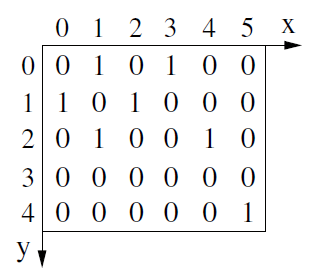
Figura 7.1: Uma matriz binária, os elementos apresentam apenas dois valores de intensidade, 0 ou 1.

Note que a notação utilizada aqui difere da notação utilizada anteriormente para as imagens em escala de cinza e coloridas em representação matricial. A origem adotada é no canto superior esquerdo, e o indíce $x$ indexa as colunas da imagem.

Como a morfologia matematica adota as operações de conjuntos, iremos revisar algumas operações fundamentais que serão utilizadas.

Sejam A e B duas imagens binárias representadas pelos conjuntos no espaço $Z^2$ com componentes $a=(a_1;a_2)$ e $b=(b_1;b_2)$, respectivamente, ou seja, pares ordenados formados pelas coordenadas dos pixels dos objetos em A e B.

• Condição: Um conjunto $A$ de coordenadas de pixels que satisfazem uma determinada condição é expresso como:

  $\begin{array}{c}A=\left\{a|\text{condição}\right\}\end{array}$

• União: O conjunto dos elementos que pertencem a $A$, $B$ ou ambos é denotada a união de $A$ e $B$, expressa como:

  $\begin{array}{c}A\cup B=\{c|c\in A\text{ou}c\in B\}\end{array}$

• Intersecção: o conjunto de todos os elementos que pertencem a ambos os conjuntos é denotado como a intersecção de $A$ e $B$, expressa como:

  $\begin{array}{c}A\cap B=\{c|c\in A\text{e}c\in B\}\end{array}$

• Translação: A translação de $A$ pelo elemento $i$, denotada $A$ + $i$, é expressa como:

  $\begin{array}{c}A+i=\{a+i|a\in A\}\end{array}$

• Reflexão: A reflexão de A, denotada $Â$, expressa como:

  $\begin{array}{c}Â=\{-a|a\in A\}\end{array}$

• Complemento: O complemento de A, denotada $\overline{A}$, expressa como:

  $\begin{array}{c}\overline{A}=\{i|i\notin A\}\end{array}$

• Diferença: a diferença de A e B, denotada como $A-B$, e expressa como:

  $\begin{array}{c}A-B=\{i|i\in (A\cap \overline{B}\left)\right\}\end{array}$

Um operador morfológico é um mapeamento entre o conjunto A que define a imagem e um conjunto B, chamado elemento estruturante, também definido em $Z^2$. O elemento estruturante pode ser pensado como uma matriz. O elemento estruturante é expresso com respeito a uma origem local.

Figura 7.2: Exemplos de elementos estruturantes.

Alguns exemplos típicos de elementos estruturantes são mostrados na imagem acima, a origem esta marcada com uma cruz (+). Os pontos pertencentes ao objeto são marcados com um círculo preenchido. É interessante notar que a origem não é necessariamente um elemento de B, como é o caso do exemplo mais a direta da figura.

A defínição formal de operações morfológicas pode ser realizada por meio da álgebra de Minkowski, em homenagem ao matemático russo Hermann Minkowski. Tal álgebra é baseada nos conceitos da teoria de conjuntos e nos operadores que revisamos acima, especialmente a união, intersecção e a complementação.

Caso o elemento estruturante B seja simétrico com respeito a sua origem, a reflexão não altera o conjunto de elementos, tal que $B=\hat{B}$.

Figura 7.3: Exemplos de elementos estruturantes simétricos e não simétricos.

O elemento estruturante a esquerda da figura é simétrico, enquanto o elemento estruturante a direita é não simétrico. É possível notar que o elemento estruturante simétrico permanece o mesmo ao ser aplicado o operador de reflexão, o mesmo não ocorre com o elementro não simétrico a direita da imagem.

A adição de Minkowski entre $A$ e $B$, denotada $A\oplus B$, e é definida como:

$\begin{array}{c}A\oplus B=\bigcup _{b\in B}A+b.\end{array}$

Um exemplo pode ser visto abaixo:

Dados os elementos $A=\left\{\right(1,1);(1,2);(1,3);(2,3);(2,4);(3,4\left)\right\}$ e $B=\left\{\right(0,0);(1,0\left)\right\}$,

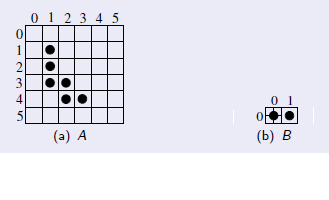
Figura 7.4: Imagem A e elemento estruturante B.

A adição de Minkowski entre A e B é dada pela união de todas as translações de A com respeito a cada elemento de B, a qual pode ser expressa como:

$A\oplus B=\left\{\right(1,1);(1,2);(1,3);(2,1);(2,2);(2,3);(2,4);(3,3);(3,4);(4,4\left)\right\}$ . O resultado, de forma gráfica pode ser visto como:

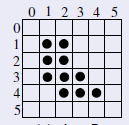
Figura 7.5: Resultado da adição de Minkowsky de A com B.

Outra forma de pensar a adição de Minkowsky de forma gráfica se utiliza de uma técnica de janela deslizante. Para isso, imagine que o elemento estruturante é posicionado sobre a imagem A. Neste caso, o elemento estruturante seria a janela. A partir da posição (0, 0), deslize o elemento estruturante sobre as colunas e linhas da imagem A.

Para cada ponto da imagem A que está na origem do elemento estruturante, realizar a soma (preencher os círculos da imagem resultante com os círculos do elemento estruturante). Esta lógica gráfica pode ser aplicada as outras operações que veremos a seguir.

A subtração de Minkowski entre $A$ e $B$, denotada $A\ominus B$, e é definida como:

$\begin{array}{c}A\ominus B=\bigcap _{b\in B}A-b=\bigcap _{b\in \hat{B}}A+b.\end{array}$

A subtração de Minkowski entre $A$ e $B$ é dada pela intersecção de todas as translações de A com respeito a cada elemento $-b\in B$. Ou pelos elementos da reflexão de $B$, ou seja, por $b\in \hat{B}$.

Um exemplo pode ser visto abaixo:

Dados os elementos $A=\left\{\right(1;4);(2;1);(2;2);(2;3);(2;4);(3;2);(3;4\left)\right\}$ e $B=\left\{\right(0,0);(1,0\left)\right\}$,

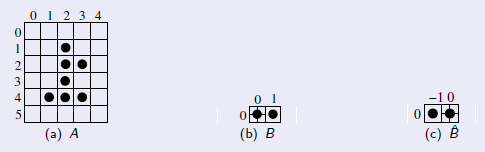
Figura 7.6: Imagem A, elemento estruturante B e reflexão do elemento estruturante B.

A subtração de Minkowski entre A e B é dada pela intersecção de todas as translações de A com respeito a cada elemento de $\hat{B}$ :

$A\ominus B=\left\{\right(1;4);(2;2);(2;4\left)\right\}$ . O resultado, de forma gráfica pode ser visto como:

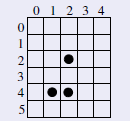
Figura 7.7: Resultado da subtração de Minkowsky de A com B.

As operações de adição e subtração de Minkowski são importantes operadores que quando aplicados a imagens binárias, correspondem respectivamente as operações de dilatação e de erosão. Denotamos a operação de dilatação da imagem $A$ com o elemento estruturante $B$ como $D(A,B)$; A operação de erosão é denotada como $E(A,B)$.

Podemos utilizar uma imagem para ilustrar os efeitos das operações de dilatação e de erosão:

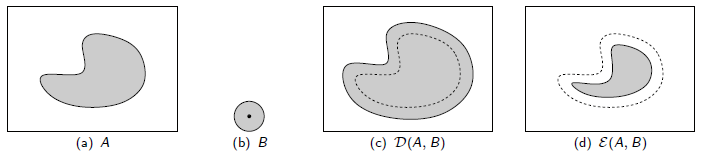
Figura 7.8: Ilustração das operações de erosão e dilatação.

O elemento estruturante B utilizado para alterar a imagem é um disco circular, cuja origem localiza-se no centro do círculo. As linhas tracejadas nas figura delimitam o contorno original do objeto na imagem e as linhas sólidas mostram o resultado após a dilatação (c) e a erosão (d). O efeito atingido faz jus ao nome das operações, onde na dilatação a forma da imagem é dilatada em relação as bordas da forma, enquanto que na erosão há o comportamento contrário. O elemento estruturante é que determina quais porções da forma são afetadas pela operação.

utilizando um dados concretos, considere o exemplo a seguir: Dado: $A=\left\{\right(1;1);(1;3);(2;1);(2;3);(2;4);(3;1);(3;2);(3;3);(3;4);(4;2);(4;3);(4;4\left)\right\}$ $B=\left\{\right(0;0);(0;1);(1;0);(1;1\left)\right\}$

representado na imagem como :

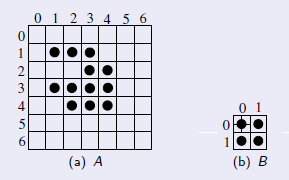
Figura 7.9: Dados de entrada das operações de erosão e dilatação.

Assim, $D(A,B)=\left\{\right(1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(2;4);(2;5);(3;1);(3;2);(3;3);(3;4);(3;5);(4;1);(4;2);(4;3);(4;4);(4;5);(5;2);(5;3);(5;4);(5;5\left)\right\}$

Uma forma mais simples de visualizar o resultado da dilatação consiste em mover a origem do elemento estruturante B sobre cada pixel dos objetos na imagem binária A e atribuir o valor 1 a cada posição da imagem que é sobreposta pelo elemento estruturante. Esta é a abordagem de janela flutuante citada anteriormente.

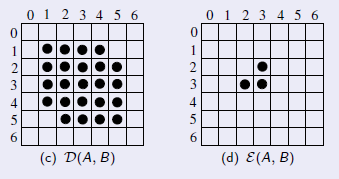
Figura 7.10: Resultado das operações de erosão e dilatação.

Assim, $E(A,B)=\left\{\right(2;3);(3;2);(3;3\left)\right\}$

Pela abordagem da janela flutuante. o resultado da dilatação consiste em mover a origem do elemento estruturante $B$ sobre a imagem $A$, tal que, caso o elemento estruturante esteja totalmente contido em $A$, o pixel da imagem sob a origem de $B$ irá pertencer à erosão entre $A$ e $B$.

As operações de dilatação e erosão também podem ser aplicadas a um elemento estruturante $B$ em que a origem do elemento nao pertencem ao conjunto $B$. A operação funciona de maneira habitual, como pode ser visto nas figuras de exemplo:

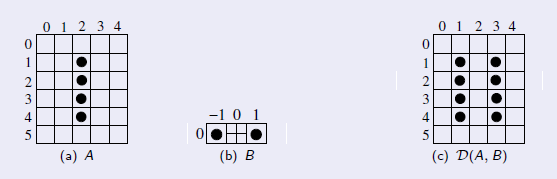
Figura 7.11: Operações de dilatação da imagem A com elemento estruturante B onde a origem do elemento estruturante não pertence a B.

Pode-se observar que os pixels dos objetos na imagem original não necessariamente pertencem a imagem resultante, ou seja, não é necessariamente um subconjunto de A.

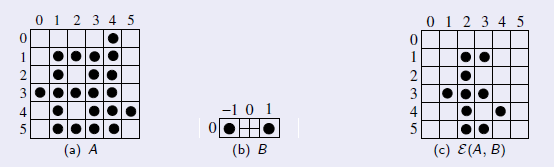
Figura 7.12: Operações de erosão da imagem A com elemento estruturante B onde a origem do elemento estruturante não pertence a B.

De maneira análoga a dilatação, os pixels na imagem resultante não correspondem necessariamente a um subconjunto de A. Entretanto, de maneira complementar ao caso da dilatação, aqui a origem do elemento estruturante não corresponde necessariamente a um pixel na imagem A

Outros operadores morfológicos muito utilizados são os operadores de abertura e de fechamento.

A abertura de $A$ por $B$, denotada $A\circ B$, é definida como:

$\begin{array}{c}A\circ B=(A\ominus B)\oplus B\end{array}$

Ou seja, a abertura de A por B é definida como a erosão de A por B, seguida de uma dilatação do resultado por B. A abertura geralmente é utilizada para suavizar o contorno de objetos, eliminar conexões estreitas entre objetos e remover saliências ou protusões finas.

Já o fechamento de $A$ por $B$, denotada $A\bullet B$, é definida como:

$\begin{array}{c}A\bullet B=(A\oplus B)\ominus B\end{array}$

Ou seja, o fechamento de A por B é definida como a dilatação de A por B, seguida de uma erosão do resultado por B. O fechamento é utilizado para fundir separações estreitas entre objetos, eliminar1 pequenos buracos e preencher lacunas no contorno.

Logo:

$\begin{array}{cc}A\circ B& =D\left(E\right(A,B),B)\\ A\bullet B& =E\left(D\right(A,B),B)\end{array}$

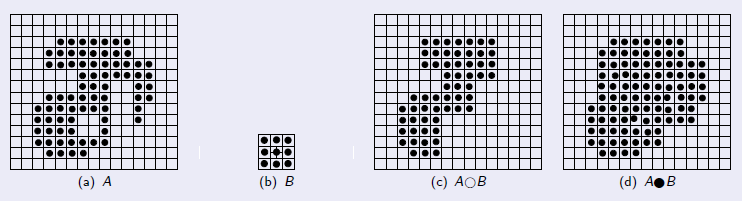
Figura 7.13: Operações de abertura e fechamento da imagem A com elemento estruturante B.

A figura acima mostra de forma gráfica exemplos do operador de abertura e fechamento. Note que a operação de abertura remove regiões que são menores ou mais estreitas que o elemento estruturante, enquanto o operador de fechamento faz a união de pequenos buracos e regiões onde há separações menores que o elemento estruturante.

Exercício

Implemente as operações de abertura e fechamento e replique o primeiro exemplo dado anteriormente.

Primeiro crie uma imagem binário seguindo a matriz $A$ do exemplo.

Em seguida, implemente as funções de dilatação e erosão. utilizando os comandos cv.erode(imagem, elemento) e cv.dilate(imagem, elemento)

Utilizando as funções de dilatação e erosão criadas anteriormente, implemente as operações de abertura e fechamento.

Confira se seu resultado está correto, utilizando a função cv.morphologyEx com os parâmetros cv.MORPH_OPEN e cv.MORPH_CLOSE

Exercício

Teste as operações de abertura e fechamento em uma imagem de sua escolha:

Primeiro carregue uma imagem em escala de cinzas e converta essa imagem para uma imagem binária. Isto pode ser feito utilizando a função ret, imagem_binaria = cv.threshold(imagem_original, 127, 255, cv.THRESH_BINARY)

Realize combinações de fechamento, abertura, erosão e dilatação, complemento e diferença a fim de analisar os diferentes efeitos alcançados.